[Advanced Statistical Computing] Julia Introduction 2

Matrices and Vectors

Dimensions(차원)

x = randn(5,3)

size(x) # (5,3) : 전체 차원 수
size(x, 1) # 5 : 행의 수
size(x, 2) # 3 : 열의 수
length(x) # 15 : 전체 성분의 수

Indexing(인덱싱)

x = randn(5,5) # 5x5 행렬

x[:, 1] # 1st column
x[1, :] # 1st row
x[1:2, 2:3] # sub-array / 1~2행, 2~3열 선택

파이썬과 다르게, 줄리아에선 인덱싱을 할 때 마지막 번호의 인덱스가 제외되지 않는다.

Copy

z = x[1:2, 2:3]

# 같은 코드
z = view(x, 1:2, 2:3)
@views z = x[1:2, 2:3]

위의 두 코드 모두 z에 x 부분행렬을 저장하게 되는데, 두 방법에는 차이가 있다.
z = x[1:2, 2:3] 의 경우에는 메모리를 새롭게 할당(allocate)하여 z라는 변수에 x의 부분행렬을 저장하는 것이지만, z = view(x, 1:2, 2:3) 의 경우엔 같은 포인터를 가리키는 하나의 변수로서 z를 이용하게 된다.

z[2,2] = 0.0

z의 2행 2열 성분을 초기화하면,

x # z = x[1:2, 2:3]

5×5 Matrix{Float64}:
  1.56701    0.11162     1.50172   -1.04396    0.271254
 -0.385128  -0.0208861   0.726587   0.155334   1.78307
  1.85628   -1.35106    -0.474294  -0.29979   -0.629733
 -0.878317   0.640118   -0.700664   0.467584  -0.289654
 -0.946056  -0.40254    -0.594829   0.857244  -0.527352

x의 성분은 변하지 않는다.

x # z = view(x, 1:2, 2:3)

5×5 Matrix{Float64}:
  1.56701    0.11162     1.50172   -1.04396    0.271254
 -0.385128  -0.0208861   0.0        0.155334   1.78307
  1.85628   -1.35106    -0.474294  -0.29979   -0.629733
 -0.878317   0.640118   -0.700664   0.467584  -0.289654
 -0.946056  -0.40254    -0.594829   0.857244  -0.527352

x의 성분도 z와 함께 변경된 것을 확인할 수 있다. C/C++ 에서 나오는 깊은 복사, 얕은 복사와 비슷한 개념으로 이해할 수 있다.

mutable vs immutable

• mutable object

y = x

pointer(x), pointer(y)

(Ptr{Float64} @0x000000010df5b890, Ptr{Float64} @0x000000010df5b890)

위처럼 단순히 =연산자를 이용할 경우 같은 주소를 가리키는 변수로 x,y가 이용된다. 따라서 y의 값을 바꾸면 x의 값도 바뀌게 된다.

다른 변수에 새로운 객체를 복사하고 싶다면 copy함수를 이용한다.

z = copy(x)

pointer(x), pointer(z)

(Ptr{Float64} @0x000000010df5b890, Ptr{Float64} @0x000000010dee4ef0)

서로 다른 주소값을 갖는 것을 확인할 수 있다.

• immutable object

a = 1.0  # Float64
b = a
b # 1.0

x, y 행렬을 이용하여 실행한 코드와 차이가 없다. 하지만.,

a = 2.0
b # 1.0

행렬을 이용했을 땐 x, y에서 하나의 값만 바꿔주어도 x,y가 가리키는 값이 전부 다 바뀌었는데 a,b의 경우엔 그렇지 않음을 볼 수 있다. 위의 코드의 경우 원래 a , 1.0 의 1.0 값을 바꾼 것이 아니라, immutable object 인 2.0을 생성하고 a가 그것을 가리키게 한다고 해석할 수 있다.

x, y를 이용한 경우를 하나 더 살펴보자.

y=x

# 1st case
x .+= 1

# 2nd case
x = x +. 1

첫 번째 경우, x,y가 함께 가리키는 행렬의 값이 모두 0.1씩 증가된다. 추가적인 메모리 할당이 존재하지 않는다.

두 번째 경우, y값은 변하지 않는다. 기존의 x,y가 가리키는 행렬에 +0.1 이 된 행렬이 새롭게 메모리에 할당되고, 추가된 이 행렬을 x변수와 연결시킨다고 생각할 수 있다.

Concatenate matrices

1x3, 3x1 array 를 생성할 수 있다. 1x3의 경우엔 벡터가 아닌 행렬의 type을 갖는다.

# 1-by-3 array
[1 2 3]

1×3 Matrix{Int64}:
 1  2  3

# 3-by-1 vector
[1, 2, 3]

3-element Vector{Int64}:
 1
 2
 3

tuple의 형태로 여러가지 변수에 다양한 행렬을 저장할 수 있다.

x, y, z = randn(5, 3), randn(5, 2), randn(3, 5)

각각의 행렬을 간단하게 결합할 수 있다. 먼저 오른쪽(열방향)으로 행렬을 붙이는 방법.

[x y]

5×5 Matrix{Float64}:
  0.589366   0.647846   0.0367562   1.24886   -0.870364
  0.32449   -1.31634    0.744843    0.123384   1.65133
 -1.50004   -0.471809  -0.557907    0.278123   1.56953
  1.19435   -0.97093    0.276958    0.870534   0.679907
 -0.226598   0.153244  -0.278464   -1.65743   -0.370024

이번엔 행렬을 아래로 붙이는 방법이다. 각각의 행렬을 간단하게 결합할 수 있다. 먼저 오른쪽으로 행렬을 붙이는 방법.

[x y; z]

8×5 Matrix{Float64}:
  0.589366    0.647846   0.0367562   1.24886   -0.870364
  0.32449    -1.31634    0.744843    0.123384   1.65133
 -1.50004    -0.471809  -0.557907    0.278123   1.56953
  1.19435    -0.97093    0.276958    0.870534   0.679907
 -0.226598    0.153244  -0.278464   -1.65743   -0.370024
  0.0334893   0.122393   1.5489     -1.6728     0.502726
 -0.371728   -0.543823  -0.71427    -0.703464   1.34872
  0.0490278   0.238179   0.122957   -0.516166  -0.0853537

;기호 다음에 온 행렬을 기존 행렬의 아래로(행방향) 붙이게 된다.

Dot operation

x = randn(5, 3)
y = ones(5, 3)

x .* y
x .^ 2
sin.(x)

위 코드 실행 결과는 x각 성분에 적용된다. 예를들어, sin.(x)의 경우 x의 모든 성분에 대해 sin 함수가 적용된다. 그냥 sin을 경우 에러 발생.

Linear algebra

x = randn(5)
y = randn(5)

5-element Vector{Float64}:
 0.34146810589642673
 1.4981812185148902
 0.25078117390294813
 0.8568548966734539
 0.2612026843555233

LinearAlgebra 패키지 사용.

Pkg.add("LinearAlgebra")
using LinearAlgebra

# L2 norm / sum(abs2, x) == sum(x.^2)
norm(x)
sqrt(sum(abs2, x)) 

# 행렬 곱
dot(x, y) # x' * y
x'y # x' : transpose

x,y = randn(5,3), randn(3,2)
x * y


# trace, determinant, rank
tr(x)
det(x)
rank(x)

참고 : 행렬 곱의 경우, 변수 이름과 혼동되지 않는 선에서 $X\beta$ 등으로

Sparse matrices

SparseArrays 패키지 사용.

• Sparse matrix 란? Sparse matrix(희소행렬)은 일부의 값만 0이 아니고, 대부분의 값이 0인 행렬을 의미한다. 희소행렬의 경우 행렬의 차원은 매우 큰 것에 반해, 0이 아닌 값이 매우 적으므로 기존의 방식대로 행렬을 저장하는 것은 비효율적인 메모리 사용을 초래한다.

using SparseArrays

# 10-by-10 sparse matrix with sparsity 0.1 / sparsity 클수록 0이 아닌 값의 비율이 증가
x = sprandn(10, 10, .1)

10×10 SparseMatrixCSC{Float64, Int64} with 5 stored entries:
   ⋅         ⋅          ⋅    ⋅    ⋅   -0.408397   ⋅   1.71158   ⋅        ⋅ 
   ⋅       -0.0276733   ⋅    ⋅    ⋅     ⋅         ⋅    ⋅        ⋅        ⋅ 
   ⋅         ⋅          ⋅    ⋅    ⋅     ⋅         ⋅    ⋅        ⋅        ⋅ 
   ⋅         ⋅          ⋅    ⋅    ⋅     ⋅         ⋅    ⋅        ⋅        ⋅ 
   ⋅         ⋅          ⋅    ⋅    ⋅     ⋅         ⋅    ⋅        ⋅        ⋅ 
   ⋅         ⋅          ⋅    ⋅    ⋅     ⋅         ⋅    ⋅        ⋅        ⋅ 
 -1.39109    ⋅          ⋅    ⋅    ⋅     ⋅         ⋅    ⋅        ⋅        ⋅ 
   ⋅         ⋅          ⋅    ⋅    ⋅     ⋅         ⋅    ⋅        ⋅        ⋅ 
   ⋅         ⋅          ⋅    ⋅    ⋅     ⋅         ⋅    ⋅       1.49509   ⋅ 
   ⋅         ⋅          ⋅    ⋅    ⋅     ⋅         ⋅    ⋅        ⋅        ⋅ 

위의 희소행렬의 .에 0을 대입한 행렬을 만들 수 있다.

Xfull = convert(Matrix{Float64}, X) # sparse(Xfull) 이용하면 원래대로 돌릴 수 있다.

10×10 Matrix{Float64}:
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0   0.0      0.0
 0.0  0.0  -2.05379  0.0  0.0  0.0  0.0  0.0   0.0      0.0
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0   0.0      0.0
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0   0.0      0.0
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0   0.0      0.0
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0   0.0      0.0
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0   0.0      0.0
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0   0.0      0.0
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0  -1.12422  0.495726
 0.0  0.0   0.0      0.0  0.0  0.0  0.0  0.0   0.0      0.0

Control flow and loops

여러가지 loop 문

• if-elseif-else-end

    if condition1
        cond1 맞으면 실행될 코드
    elseif condition2
        cond2 맞으면 실행될 코드
    else
        cond1, cond2 조건 이외의 상황에서 실행될 코드
    end
  

  
  

• for loop

    for i in 1:10
        println(i)
    end
  

  for 문의 연속 진행과 종료는 continue,break문을 그대로 다른 언어에서 처럼 똑같이 사용하면 된다.

• nested for loop

  아래 둘은 같은 for loop

    for i in 1:10
        for j in 1:5
            println(i*j)
        end
    end
  

    for i in 1:10, j in 1:5
        println(i * j)
    end
  

Functions

Julia에서 함수의 정의는 기본적으로 아래와 같이 한다.

function func(req1, req2; key1=dflt1, key2=dflt2)
    # 실행될 코드
    return out1, out2, out3 # 튜플 형태로 여러가지 값을 리턴 가능.
end

req1, req2 : 꼭 입력해주어야 하는 input 변수
; : 함수 호출시엔 입력하지 않아도 된다.
key1, key2 : default 값이 정해진 input 변수. 함수 호출 시 입력하지 않아도 된다.
return : optional. R과 같이 함수의 마지막 코드는 return 값이다.

Ex)

function myfunc(x)
    return x^2
end

x = rand(1:10, 5, 3)
myfunc.(x)

함수는 .을 이용해 vectorized 될 수 있다.

또한 함수안에 함수도 사용할 수 있다. (nested function)

• Passeed by reference vs Passed by value

  Julia는 함수에서 변수를 넘겨주는 방식이 passed by reference 방식이다.
  
  

  프로그래밍 언어의 함수가 변수를 처리하는 방식은 passed by reference와 passed by value 크게 두 가지 방식이 있는데, 지금 흐름에서 중요한 내용은 아니니 간단한 차이점만 짚고 넘어가겠다. 위에서 (x,y)행렬과 (a,b) float 객체를 가지고 복사, 포인터를 간단히 언급했는데 쉽게 말하면 그 성질들과 비슷하다.
  
  

  passed by reference : 참조(reference)에 쓰이는 포인터 개념을 이용한다고 생각하면 편하다. 주소 값을 전달하여 실제 값에 접근하는 방식이다. (x,y)행렬을 이용했을 때 처럼 값을 수정하면 원본의 데이터도 함께 수정된다
  passed by value : 값 자체를 복사하여 전달하는 방식이다. 아예 값을 복사해서 이용하기 때문에 값을 수정해도 원본의 데이터는 변경되지 않는다.

• ! (exclamation mark)

  Julia에서 함수끝에 !를 붙여주면, input argument의 값을 변경해준다. 기본적으론 passed by reference방식이라서 함수에서 사용된 input argument의 값이 변경되지 않는다.
  Ex)

    x=randn(10)
  
    sort(x)
    x
  

    10-element Vector{Float64}:
     0.9264427761518601
     0.38150426103303314
     -1.547524595940939
     -0.504552328446502
     1.2095751258044023
     -0.649869967493068
     -0.3084101818854446
     0.21178688863158096
     0.9854600549993625
     0.9119532689055165
  

  sort(x)함수를 실행했지만 인자로 전달된 x값은 바뀌지 않았다.

    sort!(x)
    x
  

    10-element Vector{Float64}:
     -1.547524595940939
     -0.649869967493068
     -0.504552328446502
     -0.3084101818854446
     0.21178688863158096
     0.38150426103303314
     0.9119532689055165
     0.9264427761518601
     0.9854600549993625
     1.2095751258044023
  

  sort!(x)함수를 실행한 이후엔 x의 값이 변경되어 있음을 알 수 있다.

• Anonymous functions

  map(x -> x^2, y) : x가 들어왔을 때 x^2을 리턴하는 mapping을 y에 적용한다고 해석할 수 있다.

• 함수의 몇 가지 형태

  • collection function ```julia # 둘 다 같은 코드 map(x -> sqrt(x), x)

  map(x) do elem elem = sqrt(elem) return elem end

    <br>
  
    * mapreduce
    ```julia
    # mapreduce(mapper, reducer, data)
    mapreduce(x -> sqrt(x), +, x)
  
    # 위와 같은 코드
    sum(x -> sqrt(x), x)
  

Type system

Any : Julia에서 모든 타입은 abstract type ‘Any’의 subtype이다.

• Number의 타입들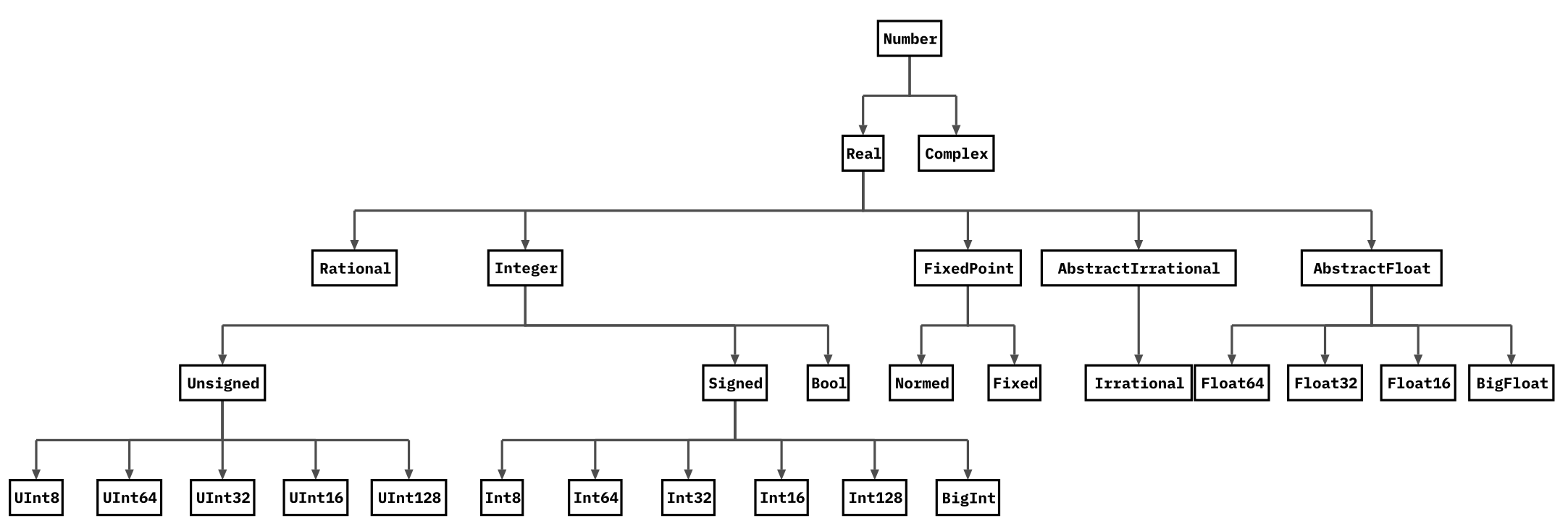

  

typeof(), supertype(), subtypes() 함수를 이용해 객체의 타입을 알 수 있다.

데이터의 타입을 변화하는 방법

convert(Float64, 1) # 1.0

x = randn(Float32, 5) # float32형 5x1 벡터
convert(Array{Float64}, x)
Float64.(x)

Multiple dispatch

간단하게 말하면, 함수에 들어오는 input argument 타입에 유연하게 적용되는 성질을 말한다. 예를 들어, 더하는 과정을 생각해보자. 2+2, 2.0+2.0 은 우리가 눈으로 보기엔 간단하지만, 프로그래밍 언어의 함수에선 매우 다른 문제이다. +함수에 들어올 수 있는 인자의 타입은 굉장이 여러가지가 있을 수 있고 각각의 경우에 대한 특정 동작을 제공함으로써 이를 구분할 수 있다. 이러한 행동의 정의를 method라고 한다.

함수가 실행될 때 메서드의 선택을 dispatch라고 한다. 들어온 인자의 타입에 따라 어떤 메서드를 이용할지가 선택된다. 함수의 인자들을 모두 이용하여 함수의 첫 번째 메서드가 아닌 메서드를 선택하는 것이 multiple dispatch로 알려져 있다. input argument의 타입이 정해지지 않은 함수를 generic function이라고 한다.

methods(function_name), @which functionc(x) 로 method를 살펴볼 수 있다.

methods(sum)

# 14 methods for generic function sum:
sum(x::Tuple{Any, Vararg{Any, N} where N}) in Base at tuple.jl:474
sum(x::AbstractSparseVector{Tv, Ti} where {Tv, Ti}) in SparseArrays at /Applications/Julia-1.6.app/Contents/Resources/julia/share/julia/stdlib/v1.6/SparseArrays/src/sparsevector.jl:1357
sum(r::StepRangeLen{var"#s79", var"#s78", var"#s77"} where {var"#s79", var"#s78"<:Base.TwicePrecision, var"#s77"<:Base.TwicePrecision}) in Base at twiceprecision.jl:553
sum(r::StepRangeLen) in Base at twiceprecision.jl:538
sum(r::AbstractRange{var"#s79"} where var"#s79"<:Real) in Base at range.jl:1068
sum(a::AbstractArray{Bool, N} where N; kw...) in Base at reduce.jl:529
sum(arr::AbstractArray{BigInt, N} where N) in Base.GMP at gmp.jl:634
sum(arr::AbstractArray{BigFloat, N} where N) in Base.MPFR at mpfr.jl:716
sum(a::AbstractArray; dims, kw...) in Base at reducedim.jl:873
sum(::typeof(abs), x::AbstractSparseVector{Tv, Ti} where {Tv, Ti}) in SparseArrays at /Applications/Julia-1.6.app/Contents/Resources/julia/share/julia/stdlib/v1.6/SparseArrays/src/sparsevector.jl:1382
sum(::typeof(abs2), x::AbstractSparseVector{Tv, Ti} where {Tv, Ti}) in SparseArrays at /Applications/Julia-1.6.app/Contents/Resources/julia/share/julia/stdlib/v1.6/SparseArrays/src/sparsevector.jl:1382
sum(a; kw...) in Base at reduce.jl:528
sum(f, a::AbstractArray; dims, kw...) in Base at reducedim.jl:874
sum(f, a; kw...) in Base at reduce.jl:501

@which sum(1,3.0)

sum(f, a; kw...) in Base at reduce.jl:501

Just-in-time compilation (dynamic tarnslation)

Julia의 컴파일 방식이다. 프로그래밍 언어는 컴파일 방법으로 크게 두 가지, Interpreter 와 compliler 가 있는데 JIT comilation 의 경우는 두 가지 방식이 섞인 것이라고 생각할 수 있다. 실행할 때 interpreter 방식으로 기계어 코드를 생성하고, 그 코드를 캐싱하여 같은 함수가 반복되면 코드를 새롭게 생성하는 것이 아니라 이미 만들어 놓은 기계어 코드를 불러와 사용한다.

몇 가지 함수를 이용하여 low level의 코드를 확인할 수 있다. 위에서 정의한 g함수를 살펴보자.

@code_lowered : AST(Abstract Syntax Tree, 추상구문트리) 보여준다.

@code_lowered g(2)

CodeInfo(
1 ─ %1 = x + x
└──      return %1
)

@code_warntype : 함수에서 쓰이는 변수들의 type을 살펴볼 수 있다.

@code_warntype g(2)

Variables
  #self#::Core.Const(g)
  x::Int64

Body::Int64
1 ─ %1 = (x + x)::Int64
└──      return %1

@code_warntype g(2.0)

Variables
  #self#::Core.Const(g)
  x::Float64

Body::Float64
1 ─ %1 = (x + x)::Float64
└──      return %1

@code_llvm : 코드를 LLVM bytecode로 컴파일
LLVM 코드는 인자의 타입에 따라 다르게 생성된다. R과 Python에선 g(2), g(2.0)이 같은 코드를 사용하지만, Julia에선 각각 Int64, Float64에 맞게 최적화된 코드를 사용한다.

@code_llvm g(2)
# shl(shift left) : 이진수 코드를 왼쪽으로 넘긴다고 생각

;  @ In[76]:1 within `g'
define i64 @julia_g_4079(i64 signext %0) {
top:
; ┌ @ int.jl:87 within `+'
   %1 = shl i64 %0, 1  # 이진수 왼쪽으로 한칸 (== 두배)
; └
  ret i64 %1
}

@code_llvm g(2.0)

;  @ In[75]:1 within `g'
define double @julia_g_4104(double %0) {
top:
; ┌ @ float.jl:326 within `+'
   %1 = fadd double %0, %0
; └
  ret double %1
}

@code_native : assembly code(lowest level)로 변환

---

[참고] :
https://won-j.github.io/M1399_000200-2021fall/, Julia Intro 2
https://juliakorea.github.io/ko/latest/manual/methods/