Permutation Test(순열 검정법)
통계학에서 가설 검정은 결국엔 어떤 집단의 분포를 파악하기 위해 이루어진다. 예를 들어 “어떤 두 분포간의 차이가 존재 하는가?” 라는 질문에 대해 일반적으로 t-test를 사용하곤 한다. 하지만 모수적(parametric) 방법인 t-test를 위해선 정상성(Normality), 독립성(Independence), 등분산성(Homogeneity) 등의 가정 만족해야 한다는 조건이 필요하다.
Permutation test(순열 검정법)는 특별한 조건 없이 사용할 수 있는 비모수적(nonparametric)인 가설 검정 방법이다. 여러 조건들이 들어 맞을 때에는 당연히 모수적 방법이 좀 더 정확하겠지만, permutation test는 데이터의 성질에 크게 의존하지 않고 사용할 수 있다는 장점이 있다.
가설 검정의 큰 틀은 크게 다르지 않다. 귀무가설 하에서, 내가 가지고 있는 데이터로 만든 통계량의 값이 얼마나 나오지 힘든 경우인지 확인해서 정말 발생하기 힘든(유의수준 이하의 확률) 사건이라면 귀무가설을 기각하는 흐름은 비슷하다. 검정을 위해 필요한 p-value의 계산을 permutation test에선 어떻게 하는지 알아보자.
처음에 permutation test를 공부할 때 이해하기 정말 쉽게 정리된 시각자료를 봤었는데 참고하면 공부하는데 도움이 될 것 같다.(THE PERMUTATION TEST / Jared Wilber)
Permutation test with two samples

두 샘플의 값들에 차이가 존재하는지에 대해 알아보고 싶다고 하자. 우선 비교의 기준을 설정해야 하는데, 두 집단의 표본 평균을 비교하는 것으로 생각하자. 위 그림을 예시로 들면 11개의 A, 9개의 B값에 대한 표본 평균을 계산할 수 있고, 두 표본 평균의 차이인 D를 우리의 검정통계량으로 사용한다.
\[T = \overline{X}_A - \overline{X}_B\]이제 우리의 검정통계량 값인 $D$가 귀무가설 하에서, 얼마나 나오기 힘든 극단적인 값인지 판단해야한다. t-test같은 모수적 방법에선 검정통계량이 귀무가설에서 가정된 어떤 분포 안에서 얼마나 끝쪽에 위치하는지를 확인해서 p-value로 기각 여부를 판단한다.
Permutation test에선 이 p-value 계산 방식에 차이가 있다. 우선 상황이 귀무가설을 따른다면 두 집단은 동일한 분포를 따른다. 따라서 나눠진 A,B에 상관없이 두 집단이 섞이더라도 표본 평균에는 큰 차이가 없어야 할 것이다. 즉, 두 집단을 랜덤하게 섞어서 표본 평균의 차이($T^*$)를 구한다면 그 값이 0에 가까운 값 근처로 분포할 것이라는 생각을 할 수 있다. 예를 들어
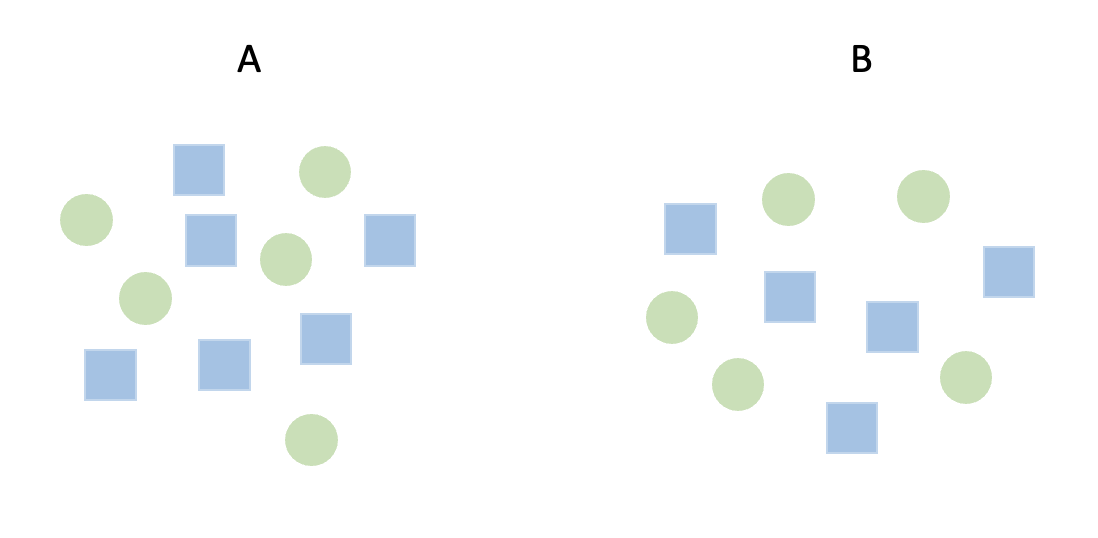
전체 데이터를 임의로 섞어서 A,B로 분류해주고 새로운 통계량 $T^*$를 계산한다. 여기서 데이터를 분류할 때, 기존의 A,B의 데이터 수에 맞게 나눠줘야한다.
조금 더 생각해보면 데이터의 크기를 $n$이라고 하고 A,B 데이터의 수를 각각 $n_A, n_B$라고 할 때, 샘플링의 가능한 경우의 수는 ${n \choose n_A} = {n \choose n_B}$로 정해져있다. 모든 경우의 수에 대한 통계량을 구해서 검정을 할 수도 있겠지만, n이 매우 커지면 그 숫자가 굉장히 커지기 때문에 그것은 비효율적이다. 따라서 전체 경우의 수보단 작지만 충분히 큰 수 $B$를 정해 그만큼만 반복하여 통계량을 계산한다.
따라서 Permutation test에서는 위와 같이 샘플링해서 통계량을 구하는 과정을 B번 반복한다고 할 때, p-value를
\[\begin{align*} \text{p-value } &= \frac{\sum^B_{b=1} I(|T^*_{b}| > |T|)}{B}\\ &= \frac{\text{B개의 통계량 중 } |T| \text{ 보다 큰 것의 개수}}{B} \end{align*}\]와 같이 계산한다. 데이터로 부터 구한 T 보다 큰 값들이 적다는 것은 귀무가설 하에서 우리의 통계량이 그만큼 나오기 힘든 값이라는 것을 의미하기 때문이다.
Permutation test의 과정을 정리하면,
- 검정통계량(D)를 계산한다.
- 전체 데이터를 랜덤하게 A,B로 나눈다. 이 때 A,B의 데이터 수는 원래 데이터와 같이 맞춰준다.
- 나눈 A,B에 대한 통계량($T^*$)을 계산한다.
- 2.~3. 과정을 B번 반복한다.
- p-value를 계산한 후 귀무가설의 기각 여부를 결정한다.
로 정리할 수 있다. 아래의 gif이미지(from wikipidia)에 위의 과정이 요약되어 있다.
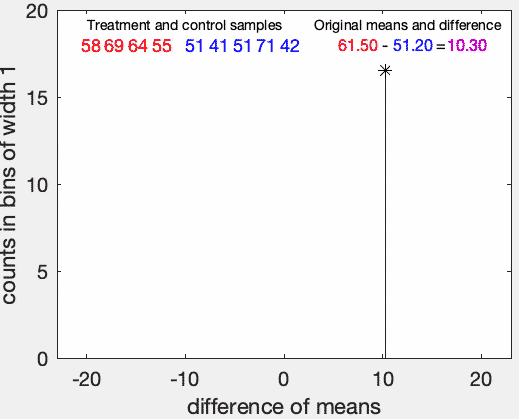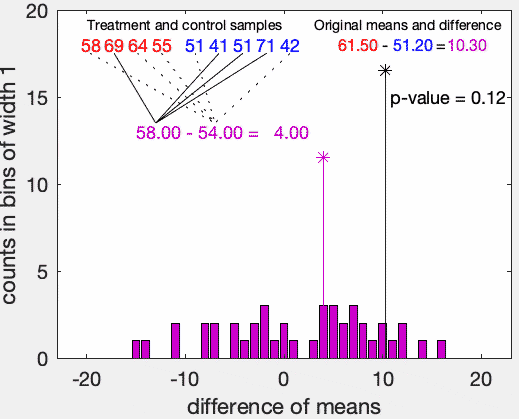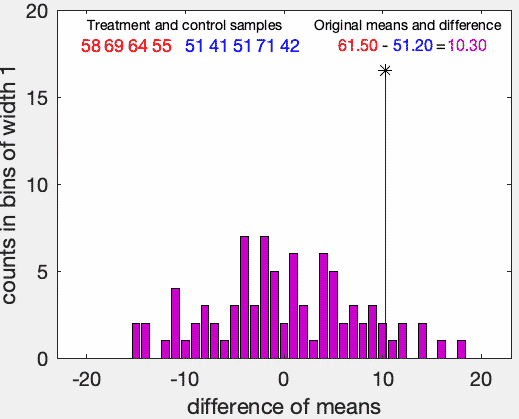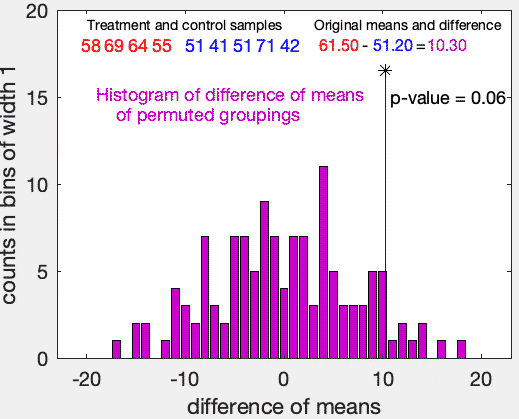
Implementation with R
[참고] :
https://www.jwilber.me/permutationtest/
https://en.wikipedia.org/wiki/Permutation_test
